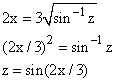
Losing a constant

In copying one line to the next, people very often omit a constant factor or sign or sometimes insert the same  factor twice. This is probably the most common error made.

Example:

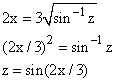
(in this case the power 2 got lost between line 2 and 3).

If you find that you make this kind of mistake, (and everyone does it,) you should check your  answer. There are two ways to do this:

1. Check each factor and power that occurs in your calculation, and see that it only disappears when cancelled with something else; and otherwise appears in the answer.

2. Check consistency of your answer by a substitution.

In this example set x = 1; then sin^-1z = 4 / 9 in the top line and z = sin(2 / 3) in the bottom; these are not consistent.

1.2 Failure to use the chain rule in differentiating or integrating

Examples

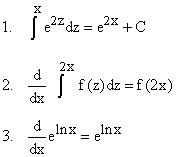
1. To find this in an integral, differentiate both sides and check.

The lhs by second fundamental theorem is

.

2. Try your integration on some function f that you can evaluate.

Thus if f = 1, the integral on the left is 2x + C; whose derivative is 2; rhs = 1; therefore the conclusion is incorrect.

3. Because such errors occur often when your mind is concentrated on the next step, always check that you have not made a chain rule error wherever you have integrated or differentiated.

1.3 Failure to read the problem accurately.

The corrective is to be sure to read each problem a second time carefully after you have started to think about it.

1.4 Varying lengths of fraction or square root symbols

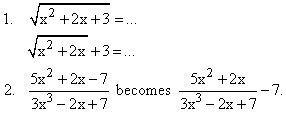
This kind of error is easier to make than it looks, on a cluttered page when you are thinking ofsomething else. Check all fraction symbols or square root for changes of this kind.

1.5 Mishandling or ignoring +C in indefinite integrals

1.6 Not drawing a proper picture of whatever is going on in the problem

1.7 Failure to cross multiply fractions properly

1.8 Failure to use the distributive law properly

1.9 Omitting - sign in derivative of cosine or integral of sine

1.10 Confusing operations; adding instead of multiplying or vice versa; integrating a polynomial instead of differentiating it or vice versa.