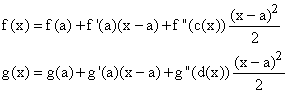
Consider the linear approximation to f(x) and g(x) at x=a:

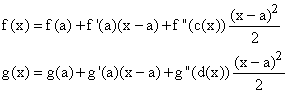
The ratio of these for x near a is:

which, if g'(a) is not 0 approaches f '(a) / g'(a) as x approaches a.

If g'(a) = 0 and f '(a) = 0 we can apply the same rule to the derivatives, to give f "(a) / g"(a).

If these second derivatives are both 0 you can continue to higher derivatives, etc. the result will be the ratio of the first pair of non-vanishing higher derivatives at a.

Of course if the first non-vanishing derivative of the numerator is the kth and occurs before the kth then the ratio is 0; if the first non-vanishing entry of the denominator occurs after that of the numerator, the ratio goes to infinity at a.