|
||
|
|
||
|
There are simple functions that have no closed form for their integrals in term of the functions:
1, x, sin x, ex
Among these are
Thus the integrals
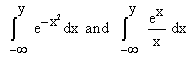
cannot be expressed as finite combinations of elementary functions. Which means we cannot do them at all.
These two functions are actually quite useful, particulary in the field of
statistics. The first of these with a normalisation factor 
is called the error function and is often tabulated. It follows (by the inverse
method) that the inverse of 
is not integrable either: this is 
.
Any integral that you can reduce to one of these if also undoable.