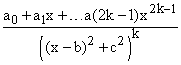In general roots of real coefficient polynomials can be real or complex. If they are complex they occur in complex conjugate pairs. If we followed the plan of integration just described for complex roots, we would have to integrate inverse powers

This can be done, but  unfortunately we have not yet defined such complex integrals.

To integrate in this case using only real integrals, we must combine together the terms from the pair of complex roots . The resulting denominators then take the form 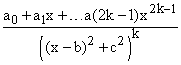 and we have to handle such terms as well as inverse powers, to integrate P(x) / Q(x) when Q has complex zeros. Luckily, integrals involving inverse powers of  with powers of x in the numerator can all be evaluated.