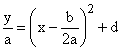The operation called "completing the square" allows us to use these formulae to do integrals in which the quadratic factor on the left here is replaced by a general quadratic, ax² + bx + c.

"Completing the square" is the act of expressing the general quadratic, y = ax² + bx + c in the form 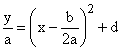 where we have .

Depending on the sign of d and the relative size of the two terms here, we get, with , one of

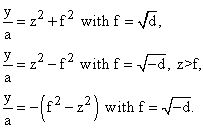
All this permits us to apply what we know about doing integrals involving these latter factors, to doing integrals involving general quadratics.

_{Comment: All quadratics look alike}

_{Example 1}

_{Example 2}