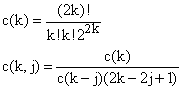We can integrate such polynomials term by term

21.4.1 Odd case

If either m or n is odd, we can make a trigonometric substitution to reduce I's integral to that of a polynomial;

suppose m is odd = 2k+1

then writing

,

we get

which can be expanded and the result integrated term by term using the product rule.

Example

21.4.2 Even case

If both m and n are even, there are three different approaches that can be used to integrate I. 

Suggested method

Use the identities

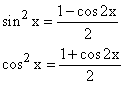
to reduce I to a polynomial of degree (m + n) / 2 in cos2x; the odd terms of this polynomial can be integrated by the previous method, the even terms reduced to a polynomial of degree at most (m + n) / 4 in cos4x, and so on.

Example

Alternate method I: Demoivre

Use DeMoivre's theorem:

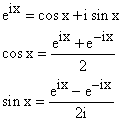
to reduce I to a sum of imaginary exponential which can be integrated like any other exponentials and then regrouped to form sines and cosines again; or regrouped into sines and cosines and then integrated.

Example

Alternate method II: Integrating by parts

Integrate by parts to reduce the integrand from cos^2kx to cos^2k-2x.

You can deduce an ugly formula for from the resulting relation.

du = cosxdx;     v = cos^2k-1x

u = sinx;            dv = -(2k-1)cos^2k-2xsinxdx

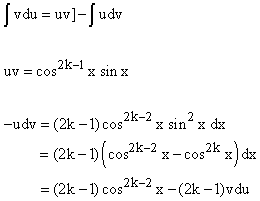
Therefore on iding by 2k, we get

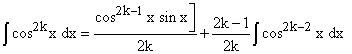
Formulae

The formula obtained in the last method 

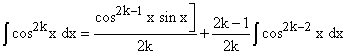
gives rise to the following results:

where

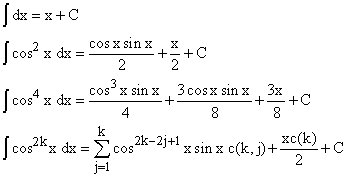
Example