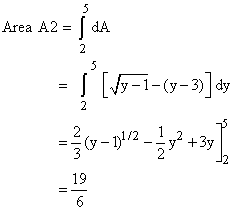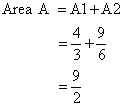|
||
|
|
||
|
Find the area A between the curves
y = 1 + x2
y = 3 + x
Introduction
To find the area between two curves you should first find out where the curves meet, which determines the endpoints of integration.You can then divide the area into vertical or horizontal strips and integrate.
Sketch the area and find points of intersection
We sketch the area to be calculated by sketching the two curves and finding their points of intersection M and N.
To find M and N, we solve:
1 + x2 = y = 3 + x
x2 -x - 2 = 0
(x - 2)(x + 1) = 0
M: x = -1 ![]() y = 2
y = 2
N: x = 2 ![]() y
= 5
y
= 5
Method of vertical strips
We divide the area A into thin vertical strips of width dx, height (3 + x) - (1 + x2) and integrate from x = -1 to x = 2.
The area dA of a vertical strip is:
dA = [(3 + x) - (1 + x2)]dx
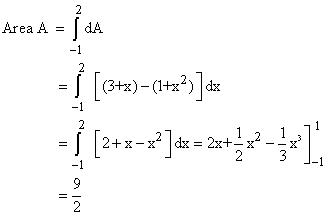
Method of horizontal strips
We divide the area A into thin horizontal strips of height dy and consider two cases to calculate their width.
Area A1: 1 < y < 2
The area dA of a horizontal strip is:
![]()
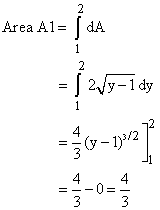
Area A2: 2 < y < 5
The area dA of a horizontal strip is:
![]()