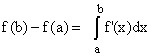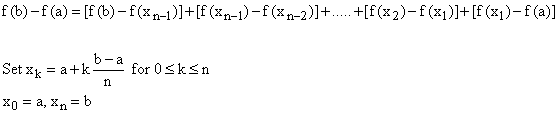
|
||
|
|
||
|
We write f(b) - f(a) as the sum of the difference of f over many little intervals xk - xk-1
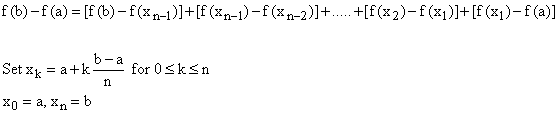
We apply the mean value theorem on each small interval
![]()
This yields, 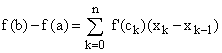 for
some ck in the kth interval for each k.
for
some ck in the kth interval for each k.
This is a Riemann sum for integrand f '(x), limits a and b, and variable of integration x, for any n.
By taking the limit as ![]() ,
we get
,
we get