We define the area under a curve formally as follows. This definition involves only the values of the integrand and does not presuppose any algebraic formula for it.

Step 1

Break the interval between a and b into n equal parts, each of width .

Comment

Step 2

Pick a point in the kth part.

Step 3

Estimate the area by the sum of the areas of the n rectangles:

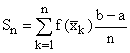
If no matter how we choose , the sum converges to the same value, that value is the integral.

Any sum S_n of this form is called a Riemann sum.

Comment