This method is used to solve an equation, which we write in the form f(x)=0, when f is differentiable.

Step 1

Start at some point x₁

Find the point x₂ where the tangent line to f at x₁ meets the x-axis.

Calculation of x₂:

The equation of the tangent line at x₁ is

y = f(x₁) + f '(x₁)(x - x₁)

x₂ solves

0 = f(x₁) + f '(x₁)(x-x₁)

Step 2

Repeat this step with x₂ and so until f(x_k) = 0

This method can be used to solve f(x) = h(x) (Just apply Newton's method to solve g(x) = f(x) - h(x) = 0.)

Comment

Application to tin cans

Illustration

Find a solution of f(x) = x³ - 3x² + 1 = 0

Curve and iterations

f(x) = x³ - 3x² + 1

f '(x) = 3x² - 6x

hence

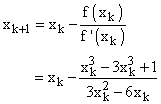
Step 1

We start at x₁ = 35

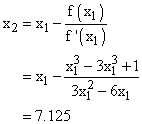
Step 2

We repeat this step with x₂ and so on...