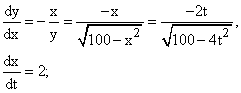
|
||
|
|
||
|
You drag the end of a 10 feet ladder along the ground at a rate of 2 ft/s.
How fast is its top along a wall descending as a function of time, given it started vertical at t =0?
x2 + y2 = 100, x = 2t until t = 5.
2xdx + 2ydy = 0
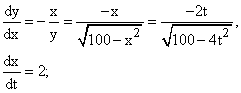
which gives the chain rule:
![]()