Minimize the surface area A of a tin can of fixed volume V.

Area of the tin can A = 2p(r²  + rh)

Volume of the tin can: V =pr²h

We minimize fixed

Compute partial derivatives

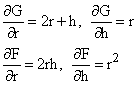
The critical condition  becomes

r²(2r + h) = 2r²h or 2r = h

G is minimized with F fixed when 2r = h.

(you must check that the endpoint behavior is consistent with the critical point being the minimum for G. If h goes to 0 then r must get large to keep V fixed, so that A goes to infinity. If r goes to 0 then h must behave as 1/r² so that again A goes to infinity.)