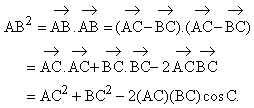The easiest way to prove this is by using the concepts of vector and dot product.

We represent a point A in the plane by a pair of coordinates, x(A) and y(A) and can define a vector associated with a line segment AB to consist of the pair (x(B)-x(A), y(B)-y(A)).

A vector consists of a pair of numbers, (a,b); the dot product of two vectors (a,b) and (c,d) is the quantity ac + bd.

The Pythagorean Theorem tells us that  the square of the length of a line segment is the dot product of its vector with itself.

In general the dot product of two vectors is the product of the lengths of their line segments times the cosine of the angle between them.

Moreover, if ABC is a triangle, the vector obeys

Taking the dot product of with itself, we get the desired conclusion.