1. The definitions here are exactly equivalent to the usual ones, that sinx is opposite over hypotenuse for a right triangle, viewed from acute angle x.

2. We measure angles in radians, for which x is the distance around the unit circle subtended by an angle x.

3. All the properties of sines and cosines easily follow from the representation e^ix = cosx + isinx.

The the Pythagorean Theorem is the statement e^ixe^-ix = e⁰ = 1;

The periodicity condition follw from the fact that ;

The addition theorems are the statement that e^i(x+y) = e^ixe^iy.

The expansions

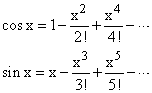
also follow immediately as do the relations

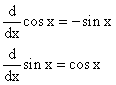
The periodicity conditions follow from the fact that ;

The addition theorems are the statement that e^i(x+y) = e^ixe^iy

Since cos has the real (that is even) terms of the series for e^ix, we can write

and similarly,