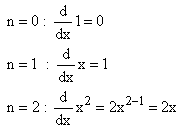The following rules allow us to find algebraic formulae for the derivative of most differentiable functions we know how to write down.

3.1.1 Derivative of Constant Function

, for any constant c  Proof of 1

3.1.2 Derivative of Identity Function

 Proof of 2

3.1.3 The Sum Rule

Proof of sum rule

Example of sum rule

3.1.4 The Product Rule

In particular

Proof of product rule

Example of product rule

3.1.5 The Chain Rule

y = f(u), u = g(x), f and g differentiable.

Then

Example of chain rule

Proof of chain rule

3.1.6 Implicit Differentiation

Suppose the function f(x) is defined by an equation: g(f(x),x)=0, rather than by an explicit formula.

Then g is a function of two variables, x and f.

Thus g may change if f changes and x does not, or if x changes and f does not.

Let the change in g arising from a change, df, in f and none in x be a(f,x)df, and let the change in g from a change, dx, in x and none in f be b(f,x).

The total change in g  must vanish since g is a constant, (0), which gives us

a(f,x)df + b (f,x)dx = 0

or

Comment on implicit differentiation

Examples of implicit differentiation

3.1.7 The Quotient Rule

In particular,

Proof of quotient rule

Example of quotient rule

3.1.8 The Power Rule

for any power n, integer, rational or irrational.

hence,

implies

Proof of power rule

Example of power rule