2.2.1 Limits

A sequence is said to approach x₀ or converge to x0 from below if it converges to x₀and all its member are less than x₀.

We say that the limit of f from below at x₀ is h, written as , if for any sequence {xj} that approaches x₀ from below, {f(xj)} approaches h.

Similarly the limit of f from above at x₀ is h, written as , if for any sequence {xj} that approaches x₀ from above, {f(xj)} approaches h.

We write when the limits from above and below are both h.

With these definitions, we can prove that if

then

Proof of 1

Proof of 2

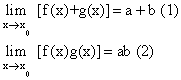
Thus the limit of sum is the sum of the limits of the terms summed; and the limit of a product is the product of the limits of its factors, (when they exist).

2.2.2 Continuity

A function f is continuous at x = x₀ if exists and is f(x₀).

A continuous function has the property that it has no "gaps" that is:

if it takes on values a and b, it takes on every value between them.

Most functions we encounter are continuous almost everywhere.

Proof