Discontinuities of this kind have infinite derivatives at the point of discontinuities and can lead to problems with integration as well. The difficulties with integration are sometimes avoidable , because the area under a curve may be finite even if the curve goes to infinity. This does not happen form the function , the area under which is infinite for x > 0.

However, if we want to integrate from a to b with a<0 and b>0, this can be defined, using the fact that the infinite part above 0 cancels symmetrically with the infinite part below.

Thus you can define the "principal part" of the integral by excluding the contribution from -c to c in the limit as c goes to 0.

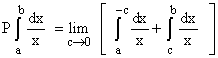 which limit exists.