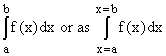Integration is the process of determining the area  bounded by a function f, the x - axis and two lines, x = a and x = b with a < b, with a negative sign associated with the contribution to it when f < 0.

a is called the lower endpoint and b the upper endpoint of  this signed area or integral, which  is denoted by .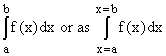

Any function continuous on the closed interval [a,b] has a well defined integral.

1. If f is differentiable on [a,b], the integral of the derivative of f from a to b is f(b) - f(a).

2. If f is continuous on [b,c] with c > b, the derivative of the integral of f, with respect to the upper limit variable c, is f(c).